Nachrichtentechnik

Dieses breite Themengebiet ist das interessanteste Beschäftigungsgebiet innerhalb unseres Ingenieurbüros. Theoretische Berechnungen, Entwurf elektronischer Schaltungen und Prototypenbau gehören hier zu unseren Tätigkeitsfeldern, wobei auf ein großes Spektrum wertvoller Fachliteratur zurückgegriffen werden kann. Das Motto lautet hier: "Je mehr über die Theorie bekannt ist, desto geringer ist der Unterschied zur Praxis!"

Kontinuierliche Fourier-Transformation

Berechnungen nach Laplace (Einschaltvorgänge, Sprungantwort, ...)

FFT - diskrete Fouriertransformation, komplex und reel bis zu 32768 MiB (BluRay)

CEPSTRUM-Analyse (wie FFT)

2-D-FFT - diskrete zweidimensionale Fouriertransformation und 2-D-CEPSTRUM-Analyse von Real-Daten bis zu 32768 MiB (BluRay)

Entwurf digitaler FIR-Filter (Filterkoeffizienten auf Anfrage), aktiver Filter und passiver Filter

Filterung von Abtastserien und *.wav-Dateien mit beliebig dimensionierbaren digitalen Filtern (TP, HP, BP, BS)

Filterung im Spektralbereich

Entwurf von schnellen Assemblerprogrammen (TASM, MASM32)

Entwicklung analoger und digitaler diskreter Schaltungen (Spice)

Aktive und passive Antennen, Berechnung von Anpassungen

Funkortung und Navigation

Microcontroller Embedded Systems auf Anfrage

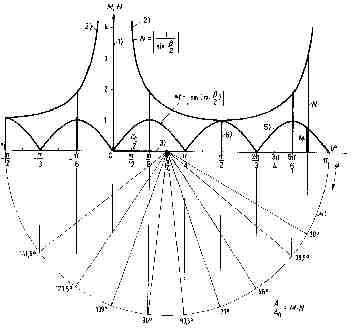
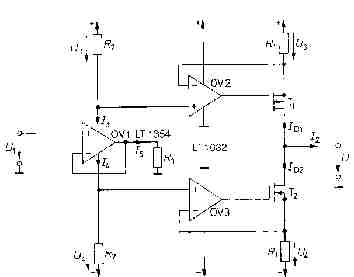
Während die Fourier-Transformation ein bekanntes Hilfsmittel der Ingenieurwissenschaften ist (die Fourier-Transformierte eines Signals im Zeitbereich s(t) ist die kontinuierliche Spektralfunktion des Signals im Frequenzbereich S(f)), ist der Begriff CEPSTRUM-Analyse (die Berechnung des CEPSTRUMS eines Signals s(t) aus dem Zeitbereich erfolgt durch die komplexe Logarithmierung der Fourier-Transformierten S(f) und anschließende inverse Fourier-Transformation) erklärungsbedürftig.

Eine Anwendung der CEPSTRUM-Analyse ist die Erkennung von Signalechos, wie sie zum Beispiel bei der Mehrwegausbreitung auftreten [Kemerait, R.C. and Childers, Signal Detection and Extraction by CEPSTRUM-Techniques, IEEE Trans. Info. Theory, Vol. IT-18, No. 6, pp. 745-759]. In unserem Büro wurde das mathematische Verfahren untersucht und abgeändert um eine amplitudenunabhängige Impulslängenbestimmung durchführen zu können, wie sie zum Beispiel praktisch in zivilen, aber vor allem militärischen RADAR-Anlagen sinnvoll erscheint. Darüber hinaus sind genaue kriminaltechnische Untersuchungen an digitalen Bildern und Tonaufzeichnungen möglich. Mathematisch und physikalisch Interessierte haben auch [hier] die Möglichkeit mit der rechten Maustaste einen Text im Format PDF herunterzuladen. Entsprechende Assemblerprogramme wurden von uns entwickelt.

CEPSTRUM-Analysen --- Sept. 2007

Die Arbeit an den Anwendungen der CEPSTRUM-Analysen habe ich für Abtastserien mit großem n eingestellt, wegen der Mehrdeutigkeit der Delta-Impulse.

Darüber hinaus möchte ich auf grundlegende Fehler von BRIGHAM in seinem Buch FFT-Anwendungen aus dem Oldenbourg-Verlag hinweisen. Die dort angegebene Möglichkeit zur Abspaltung reflektierter elektromagnetischer Wellen ist wegen der elektrotechnischen Grundlage E = SQRT(E1^2 + E2^2) falsch.

Allerdings ist es interessant, wie man mit der CEPSTRUM-Analyse die Orte der mathematischen Singularitäten finden kann, die dann durch Delta-Impulse markiert sind. Die Laplace-Transformation wurde extra entwickelt um trotz diese Singularitäten mathematisch arbeiten zu können. Den Unterschied zwischen der Fourier-Transformierten und einer Laplace-Transformierten eines Signals sind diese Delta-Impulse.